自然的Perlin噪声

噪声的生成

噪声(Noise)是一些乱七八糟、没有规律的东西，通常人们都很讨厌它们，但是在图形学里，利用噪声数据我们可以创造出一些随机的效果。不过单纯的随机数作为噪声数据会使结果看起来十分机械不自然，它们过于杂乱无章，数据之间的变化非常突兀。比如一张图片里的颜色完全随机是很难看的，但如果图片里的颜色随机，某种颜色附近都是相近的渐变色看起来就会好很多。

在 1985 年，Ken Perlin 发明了一种“柔和”的噪声，通过在离散的随机数之间进行插值，这种噪声在保留随机性的同时也实现了局部的连续性。以一维数据为例，生成噪声时在 x=1, 2, 3...这些整数位置生成随机的数值，两个整数位置之间则使用连续函数插值得到数据。在使用的时候，如果直接用整数坐标值去取值，得到的结果并不具备连续性，解决的方式很简单，对坐标进行缩放即可，比如当 x=1 时使用 x=0.01 的噪声值。

for (let x = 0; x < SIZE; x++) {
  let scale = 0.002;
  let value = noise.simplex2(x * scale, 1); // [-1, 1]
  let height = Math.ceil(((value + 1) / 2) * SIZE); // 1, 2, 3, ..., SIZE
  for (let y = SIZE - 1; y >= height; y--) {
    drawPixel(image, x, y);
  }
}

随机

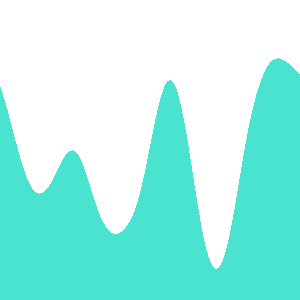插值

Perlin 发明的这种方法衍生了许多变种，尽管命名、算法各不相同但核心思想是一样的，后文中简单的统称为 Perlin 噪声。

噪声的叠加

经过插值处理的噪声数据虽然不那么突兀了，但是有些过于简单，反而不够自然。上文中使用缩放后的坐标取噪声值以确保数据的连续性，如果不进行缩放数据就是完全随机离散的，那么只要寻找一个合适的方法，把不同缩放比的噪声进行叠加，平衡连续性和随机性，就可以让结果包含更丰富的细节，显得更加自然。

为了方便的描述噪声的处理过程，我们可以把噪声看作是一种信号，对坐标进行缩放实际上是在改变信号的频率(Frequency)。噪声的值域原本都是相同的[-1, 1]，但在叠加时可给不同频率的噪声值分配一个权重实现更精细的控制，这个权重值对应了信号的振幅(Amplitude)。

既然叠加是为了得到精细的结果，频率和振幅显然不能随机设置，最常见的控制频率的方法是使相邻信号的频率比值为 2，即第 n 个噪声的频率为 2 的 n 次方。在这种规律下，人们使用一个参数 Persistence 简化对最终结果的控制，使第 n 个噪声的频率为 Persistence 的 n 次方，Persistence 越小，得到的结果越随机，越大则更单调一些。

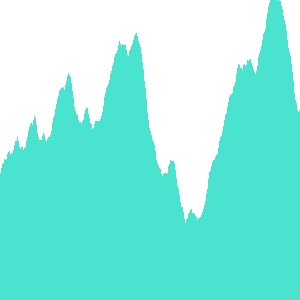叠加

在得到每个信号值后，最简单的叠加方法就是直接求和，我们还可以设计自己的叠加方法，从而得到各种各样有意思的效果。

for (let x = 0; x < SIZE; x++) {
  let frequency = 0.005;
  let persistence = 0.5;
  let amplitude = 1;
  let totalAmp = 1;
  let value = 0;
  for (let i = 0; i < 16; i++) {
    value += noise.simplex2(x * frequency, 1) * amplitude;
    totalAmp += amplitude *= persistence;
    frequency *= 2;
  }
  value /= totalAmp;
  let height = Math.ceil(((value + 1) / 2) * SIZE);
  for (let y = SIZE - 1; y >= height; y--) {
    drawPixel(image, x, y);
  }
}

应用

模拟自然现象

求和叠加

取绝对值后求和

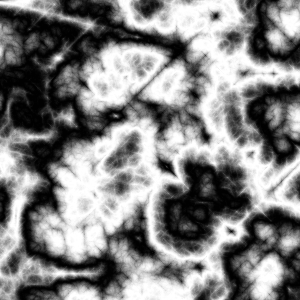使用三角函数sin

for (let x = 0; x < SIZE; x++) {
  for (let y = 0; y < SIZE; y++) {
    let value = 0;
    let freq = 0.005;
    let amp = 1;
    let totalAmp = 1;
    for (let i = 0; i < 16; i++) {
      value += noise.simplex2(x * freq, y * freq) * amp;
      amp *= 0.5;
      totalAmp += amp;
      freq *= 2;
    }
    value /= totalAmp;
    value = Math.ceil(((value + 1) / 2) * 255);
    drawPixel(image, x, y, value);
  }
}

通过各种方式叠加噪声可以得到具备自然特征的图像，使用二维噪声值作为图像灰度，直接求和叠加产生的效果有点类似云朵，如果取绝对值后再求和，就会有点像神经网络，如果再对叠加结果使用三角函数，就会出现……？。

在生成规则图案比如圆形、方形等形状时，如果引入 Perlin 噪声作为偏移，可以让这些原本规则的图案发生“扭曲”，从而对手绘的抖动、木纹、石纹等等效果进行模拟。

木纹效果，来源：Perlin噪声 - 维基百科，自由的百科全书

人们也经常用噪声来生成地形，创建起伏的地势、山脉，再给这些地形赋予其他各种各样的特征就可以得到不同的地理环境，在游戏中是十分实用的。

游戏地形，来源：Little Planet Procedural

物体运动

如果把时间作为噪声的一个维度，可以使空间位置的噪声数据自然地发生变化。

动画

function simpleWave(frame) {
  const image = ctx.createImageData(SIZE, SIZE);
  for (let x = 0; x < SIZE; x++) {
    let scale = 0.01;
    let value = noise.simplex2(x * scale, frame * scale);
    let height = Math.ceil(((value + 1) / 2) * SIZE);
    for (let y = SIZE - 1; y >= height; y--) {
      drawPixel(image, x, y);
    }
  }
  ctx.putImageData(image, 0, 0);
}
let frame = 0;
(function loop() {
  simpleWave(frame++);
  requestAnimationFrame(loop);
})();

这种自然的变化可以用来模拟火焰的摇晃，波浪的起伏。

另外一种常见的用法是通过噪声数据生成向量场，控制粒子的移动方向和速度。

一些不追求物理真实的流体效果就可以使用噪声来实现，取噪声的旋度场作为速度场可以使粒子在随机运动的同时在整体观感上具备流体的特征。